PoPL Lecture 11

• Abstract Reduction Systems
• Basically a set and a relation

• Relation composition

  

• Derived Abstract Reduction systems
• Essential idea is the simplification of programs like in high school algebra.
• Normal form: not reducible
• y is normal form of x if x → .. → y
• y is simplified of x if x → .. → y
• y is direct successor of x if x → y
• y is successor of x if x → .. → y
• x and y are joinable if x → .. → z and y → .. → z
• Properties of abstraction systems:

  • Church Rosser: ∀ a, b, if a <-> b, a and b joinable

    Example of not:

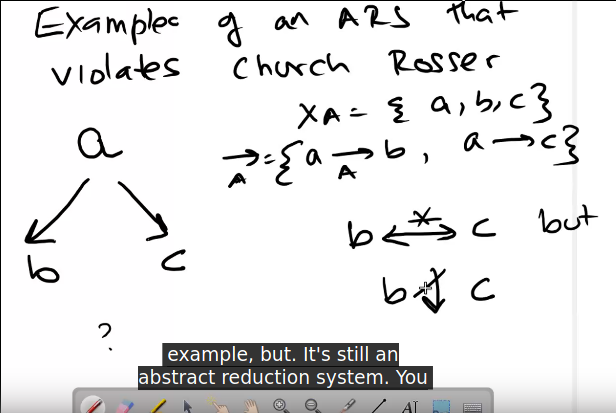
  • If system has Church rosser property, then LHS <-> RHS is possible. Simplification possible